Project Euler 85: Investigating the number of rectangles in a rectangular grid.

---

Problem Description

Investigating the number of rectangles in a rectangular grid.
By counting carefully it can be seen that a rectangular grid measuring 3 by 2 contains eighteen rectangles:

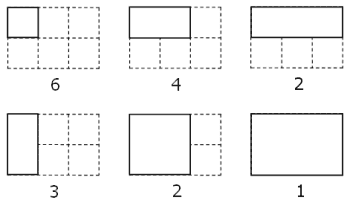
Although no rectangular grid exists that contains exactly two million rectangles, find the area of the grid with the nearest solution.

Analysis

To find the sum of the counting numbers from 1 to n is given by the formula: So, for example, the sum of the numbers from 1 to 100 is 100(101)/2 = 5050.

Counting the number of rectangles for an x by y grid is given by the formula:

This is the sum of the counting numbers 1 through x multiplied by the sum of the counting numbers 1 through y divided by 4.
In our example for x=3, y=2:

All we need to do is simply find an x and y that yield nearly 2,000,000 rectangles and calculate the area (xy).

Like so many of these problems, more consideration goes into finding and proving the search parameters than solving the actual problem but let’s guess that an upper limit of 100 will work for both x and y and write a brute force program to see if it works:

L = min_diff = 2000000;

for x in range(2, 101):
  for y in range(x, 101):
    diff = abs(x*(x + 1) * y*(y + 1) / 4 - L)
    if diff < min_diff:
      area, min_diff = x * y, diff

print "Project Euler 85 Solution =", area

It solves the problem quickly and is fairly extensible. But after looking at it for awhile we see that once a given x is chosen, the y can be derived by solving the quadratic equation:

or

So when x is known, as 3 for example:

or which solves as y = (-3,2). We are only concerned with the positive component.

Further, the search for x can be terminated once x exceeds y. This is a huge benefit because we have removed any justification required for limits and reduced the search to one loop and that loop does not have to check values that are irrelevant.

Project Euler 85 Solution

Runs < 0.001 seconds in Python 2.7.
Use this link to get the Project Euler 85 Solution Python 2.7 source.

Afterthoughts

• There are cases where a number of rectangles have many solutions and could yield different areas. One such example is 315 rectangles which yields a=28 (2 x 14) and a=30 (5 x 6).