(6 votes, average: 4.33 out of 5)
Loading...
Project Euler 140: Modified Fibonacci golden nuggets
Problem Description
Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + …, where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, … .
For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
The corresponding values of x for the first five natural numbers are shown below.
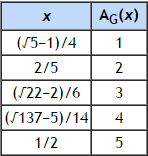
We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365.
Find the sum of the first thirty golden nuggets.
Project Euler 140 Solution
Runs < 0.001 seconds in Python 2.7.
Use this link to get the Project Euler 140 Solution Python 2.7 source.
Afterthoughts
-
No afterthoughts yet.
Project Euler 140 Solution last updated
Discussion
No comments yet.