Project Euler 139: Find how many Pythagorean triangles allow tiling with a perimeter < 10⁸

Project Euler 139 Problem Description

Project Euler 139: Let (a, b, c) represent the three sides of a right angle triangle with integral length sides. It is possible to place four such triangles together to form a square with length c.

For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.

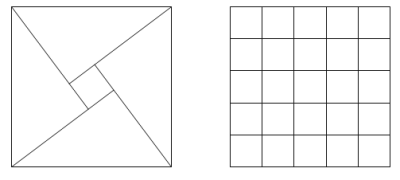
However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square.

Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?

Analysis

The paper “Tiling with Pythagorean Triples” offers a journey through the rough streets of brute forcing to the tranquil avenue of Pell’s equation. The following discussion paraphrases this excellent discussion in an effort to summarize my solution.

Using Euclid’s formula, the tiling condition can be expressed as:

We can rearrange and group the terms, and define two new variables, to transform the equation:

Since m and n are positive integers, with m > n , it follows from the above that x and y will also be positive integers. Given that, the last version of the tiling condition fits the Pell’s equation form of Diophantine equations.

A Diophantine equation is a polynomial equation with the added constraint that only integer solutions are allowed; Pell’s equation is a specific form of Diophantine equation.

Jump over to Dario’s site and solve the Diophantine equation as:

This program and method
solves all test cases
on HackerRank

Project Euler 139 Solution

Afterthoughts

No afterthoughts yet.