
Project Euler 128: Find the 2000th hexagonal tile in which the differences between it and its 6 neighbors yield 3 primes.
Problem Description
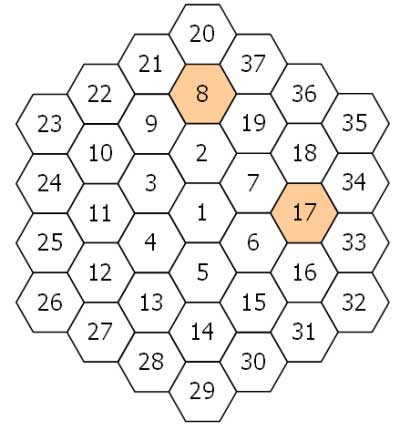
A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, starting at "12 o’clock" and numbering the tiles 2 to 7 in an anti-clockwise direction.
New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings.
By finding the difference between tile n and each its six neighbours we shall define PD(n) to be the number of those differences which are prime.
For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So PD(8) = 3.
In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence PD(17) = 2.
It can be shown that the maximum value of PD(n) is 3.
If all of the tiles for which PD(n) = 3 are listed in ascending order to form a sequence, the 10th tile would be 271.
Find the 2000th tile in this sequence.
Analysis
This is a modified version of the solution for probelm 58 – The square spiral – as this is a hex spiral constructed in the same way. As you may have guessed, just like ignoring the bottom-right diagonal in the square spiral, there are many directions we can ignore here as well as they always yield a non-prime difference (both even or both odd).
The solution below is a first swing at finding a solution. The real task is to learn of the generating function that will replace this brute force search.
Project Euler 128 Solution
Runs < 0.550 seconds in Python 2.7. Use this link to get the Project Euler 128 Solution Python 2.7 source.
Use this link to get the Project Euler 128 Solution Python 2.7 source.
Afterthoughts
-
No afterthoughts yet.

weight=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
happy=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
tothap=0
for i in range(len(items)):
weight[i] = items[i][0]
print weight
for o in range(len(items)):
happy[o] = items[o][1]
print happy
for j in range(len(weight)):
for k in range(j+1,len(weight)):
for l in range(k+1,len(weight)):
if(weight[j]+weight[k]+weight[l]) tothap:
tothap=happy[j]+happy[k]+happy[l]
print ‘tothap:’,tothap
#print weight[j], weight[k], weight[l]
#if happy[j]+happy[k]+happy[l] > tothap :
for j in range(len(weight)):
for k in range(j+1,len(weight)):
if(weight[j]+weight[k]) tothap:
tothap=happy[j]+happy[k]
print ‘tothap:’,tothap
for j in range(len(weight)):
if weight[j] tothap:
tothap=happy[j]
print ‘tothap:’,tothap
print ‘tothap:’,tothap
Posted by Thomas Stragert | September 26, 2014, 6:56 PM