Loading...
Project Euler 102: Determine if the origin is contained inside a triangle.
Project Euler 102 Problem Description
Project Euler 102: Three distinct points are plotted at random on a Cartesian plane, for which -1000 ≤ x, y ≤ 1000, such that a triangle is formed.
Consider the following two triangles:
X(-175,41), Y(-421,-714), Z(574,-645)
It can be verified that triangle ABC contains the origin, whereas triangle XYZ does not.
Using triangles.txt (right click and ‘Save Link/Target As…’), a 27K text file containing the co-ordinates of one thousand "random" triangles, find the number of triangles for which the interior contains the origin.
NOTE: The first two examples in the file represent the triangles in the example given above.
Analysis
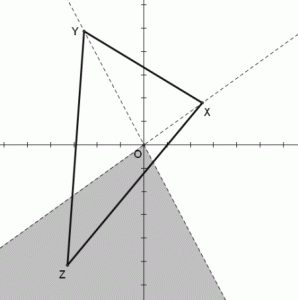There are a few ways to solve this problem. With having the point to check be the origin (0,0), then the easiest way is to check that the signs of the cross products are all positive or negative. This solution could be easily modified to check points other than the origin.
Project Euler 102 Solution
Runs < 0.001 seconds in Python 2.7.
Use this link to get the Project Euler 102 Solution Python 2.7 source.
Afterthoughts
-
No afterthoughts yet.
Discussion
No comments yet.