Loading...Analytic Proofs
Analytic proofs of geometric theorems can often be demonstrated more clearly by the use of coordinates as opposed to synthetic proofs which use deduction from axioms and previously derived theorems.
Problem 1. The Parallelogram Law
Prove analytically that the sum of the squares of the four sides of a parallelogram is equal to the sum of the squares of the
diagonals.
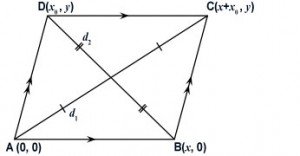
In ABCD, let d1 and d2 be the diagonals AC and BD, respectively. Construct a coordinate system so that A is the origin,
B lies on the positive x axis, and C and D lies above the x axis. See the diagram below. Assume
that AB is equal to DC and AD is equal to BC. We must prove that:
Let x be the x coordinate of B, let C have coordinates (x + x0, y) and D have the coordinates (x0, y). If x0 is 0 then the parallelogram is a rectangle.
Firstly, using the distance formula, let’s solve for the length of the two diagonals, d1 and d2.
![\setlength\arraycolsep{2pt}\begin{array}{rl} \displaystyle d_1 &= \overline{AC} \\[6pt] &= \sqrt{\left(x + x_0\right)^2 + y^2} \\[6pt] &= \sqrt{x^2 + x_0^2 + y^2 + 2xx_0} \end{array}](https://s0.wp.com/latex.php?latex=%5Csetlength%5Carraycolsep%7B2pt%7D%5Cbegin%7Barray%7D%7Brl%7D++%5Cdisplaystyle+d_1+%26%3D+%5Coverline%7BAC%7D+%5C%5C%5B6pt%5D++%26%3D+%5Csqrt%7B%5Cleft%28x+%2B+x_0%5Cright%29%5E2+%2B+y%5E2%7D+%5C%5C%5B6pt%5D++%26%3D+%5Csqrt%7Bx%5E2+%2B+x_0%5E2+%2B+y%5E2+%2B+2xx_0%7D++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0&c=20201002)
![\setlength\arraycolsep{2pt}\begin{array}{rl} d_2 &= \overline{BD} \\[6pt] &= \sqrt{\left(x_0 - x\right)^2 + y^2} \\[6pt] &= \sqrt{x^2 + x_0^2 + y^2 - 2xx_0} \end{array}](https://s0.wp.com/latex.php?latex=%5Csetlength%5Carraycolsep%7B2pt%7D%5Cbegin%7Barray%7D%7Brl%7D++d_2+%26%3D+%5Coverline%7BBD%7D+%5C%5C%5B6pt%5D++%26%3D+%5Csqrt%7B%5Cleft%28x_0+-+x%5Cright%29%5E2+%2B+y%5E2%7D+%5C%5C%5B6pt%5D++%26%3D+%5Csqrt%7Bx%5E2+%2B+x_0%5E2+%2B+y%5E2+-+2xx_0%7D++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0&c=20201002)
Now let’s sum the squares of the diagonals:
![\setlength\arraycolsep{2pt}\begin{array}{rl} d_1\!^2 + d_2\!^2 &= \left(x^2 + x_0^2 + y^2 + 2xx_0\right) + \left(x^2 + x_0^2 + y^2 - 2xx_0 \right) \\[6pt] &= 2\left(x^2 + x_0^2 + y^2\right) \end{array}](https://s0.wp.com/latex.php?latex=%5Csetlength%5Carraycolsep%7B2pt%7D%5Cbegin%7Barray%7D%7Brl%7D++d_1%5C%21%5E2+%2B+d_2%5C%21%5E2+%26%3D+%5Cleft%28x%5E2+%2B+x_0%5E2+%2B+y%5E2+%2B+2xx_0%5Cright%29+%2B+%5Cleft%28x%5E2+%2B+x_0%5E2+%2B+y%5E2+-+2xx_0+%5Cright%29+%5C%5C%5B6pt%5D++%26%3D+2%5Cleft%28x%5E2+%2B+x_0%5E2+%2B+y%5E2%5Cright%29++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0&c=20201002)
Secondly, again using the distance formula, let’s solve for the length of the two sides AB and AD.
![\overline{AB} = x \\[6pt] \overline{AD} = \sqrt{x_0^2 + y^2}](https://s0.wp.com/latex.php?latex=%5Coverline%7BAB%7D+%3D+x+%5C%5C%5B6pt%5D+%5Coverline%7BAD%7D+%3D+%5Csqrt%7Bx_0%5E2+%2B+y%5E2%7D&bg=ffffff&fg=000&s=0&c=20201002)
Finally, we want to sum the squares of the sides and multiply by 2 (4 sides total, 2 of each length).
Thus, we have proven that the sum of the squares of the four sides of a parallelogram is equal to the sum of the squares of the diagonals.
This is really clear and concise! Thank you so much for contributing this proof and helping me understand this principal.
Posted by J Bear | May 22, 2019, 2:53 PMSo’easily prove it by analytical method!
Posted by Anwez sem | September 10, 2014, 9:55 AMsuper
Posted by prabanjan | February 26, 2014, 3:45 AM