
Project Euler 68: Find the maximum 16-digit string for a "magic" 5-gon ring
Problem Description
Consider the following "magic" 3-gon ring, filled with the numbers 1 to 6, and each line adding to nine.
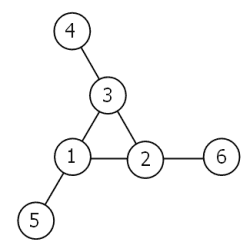
Working clockwise, and starting from the group of three with the numerically lowest external node (4,3,2 in this example), each solution can be described uniquely. For example, the above solution can be described by the set: 4,3,2; 6,2,1; 5,1,3.
It is possible to complete the ring with four different totals: 9, 10, 11, and 12. There are eight solutions in total.
| Total | Solution Set |
| 9 | 4,2,3; 5,3,1; 6,1,2 |
| 9 | 4,3,2; 6,2,1; 5,1,3 |
| 10 | 2,3,5; 4,5,1; 6,1,3 |
| 10 | 2,5,3; 6,3,1; 4,1,5 |
| 11 | 1,4,6; 3,6,2; 5,2,4 |
| 11 | 1,6,4; 5,4,2; 3,2,6 |
| 12 | 1,5,6; 2,6,4; 3,4,5 |
| 12 | 1,6,5; 3,5,4; 2,4,6 |
By concatenating each group it is possible to form 9-digit strings; the maximum string for a 3-gon ring is 432621513.
Using the numbers 1 to 10, and depending on arrangements, it is possible to form 16- and 17-digit strings. What is the maximum 16-digit string for a "magic" 5-gon ring?

Analysis
see Solution.
Project Euler 68 Solution
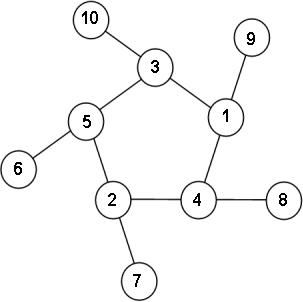
The clues “magic” (as in magic square) and 16-digit not 17-digit number give this one away. The inner and outer rings consist of 5 numbers each; the numbers from inner ring add to the sum twice, while numbers from outer ring only once.
Using the example, the bigger numbers go on the outside and the smaller numbers on the inside would yield a “magic” sum as ((6+7+8+9+10) + 2*(1+2+3+4+5))/5 = 14.
They total 14 from all views, and, following the instructions above:
Working clockwise, and starting from the group of three with the numerically lowest external node, each solution can be described uniquely.
On our first try we discovered the answer and have included it below, so don’t look if you want to face the challenge yourself.
Afterthoughts
- Looking for more trouble? Try this one:
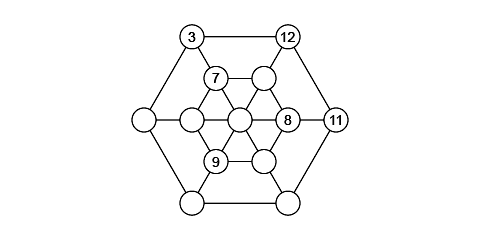
Nadejda Dyakevich’s Magic Double Hexagon
Instructions: Fill in the circles so that the sum of all numbers along each of the three diagonals and each of the two concentric hexagons is equal to 39. Use only numbers 1 through 13 inclusively with no repetitions.


Discussion
No comments yet.