Project Euler 173: Using up to one million tiles find many different "hollow" square laminae can be formed.

Problem Description

We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry. For example, using exactly thirty-two square tiles we can form two different square laminae:

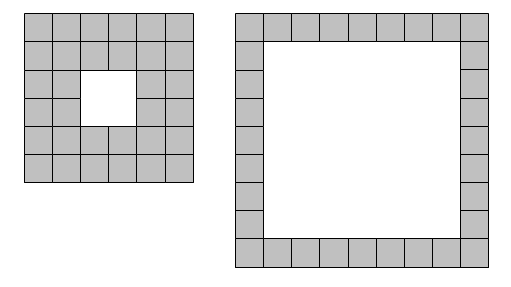
With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae.

Using up to one million tiles how many different square laminae can be formed?

Analysis

Ran a brute force for the first 10,000 tiles and found the series. So the next step is to form a generating function to calculate the answer, but, alas, this is unlikely to ever happen.

Project Euler 173 Solution

Afterthoughts

• See also, Project Euler 174 Solution: