
Project Euler 138: Investigating isosceles triangle for which the height and base length differ by one.
Problem Description
Consider the isosceles triangle with base length, b = 16, and legs, L = 17.
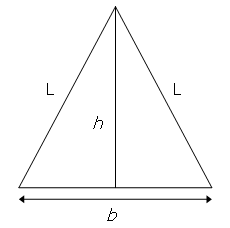
By using the Pythagorean theorem it can be seen that the height of the triangle, h = √(172 − 82) = 15, which is one less than the base length.
With b = 272 and L = 305, we get h = 273, which is one more than the base length, and this is the second smallest isosceles triangle with the property that h = b ± 1.
Find ∑ L for the twelve smallest isosceles triangles for which h = b ± 1 and b, L are positive integers.
Analysis
There are two ways to solve this problem. The first is to generate some triangles that match the requirements and search for an integer sequence; which we found. It turns out that one-half of every 6th iteration of the Fibonacci sequence, starting at the 9th, yields a solution for L. Namely: 34, 610, 10946, 196418, etc. or F(6n+3), n=1..12.
The second way, and actually more intuitive, is to solve for the Diophantine quadratic equation as:
(assuming x for b/2 to achieve integer coefficient for the resulting equation)
Take a run over to: http://www.alpertron.com.ar/QUAD.HTM, and plug in the coefficients to calculate:
5 x2 - y2 + 4 x + 1 = 0 by Dario Alejandro Alpern X0 = 0 Y0 = -1 and also: X0 = 0 Y0 = 1Xn+1 = P Xn + Q Yn + K Yn+1 = R Xn + S Yn + L
P = -9 Q = -4 K = -4 R = -20 S = -9 L = -8
We verified this solution, but never had the need to implement it.
Project Euler 138 Solution
Runs < 0.001 seconds in Python 2.7. Use this link to get the Project Euler 138 Solution Python 2.7 source.
Use this link to get the Project Euler 138 Solution Python 2.7 source.
Afterthoughts
- Reference: The On-Line Encyclopedia of Integer Sequences (OEIS) A007805: a(n)=F(6n+3)/2, where F=the Fibonacci sequence.

Clearly the constant parameter should be 2, not 1.
For 2 Dario’s website says there are no answers, care to explain how exactly you’ve verified that solution?
Posted by David | August 23, 2012, 2:46 PMNevermind, my mistake
Posted by David | August 23, 2012, 2:48 PMNo problem. Glad you worked it out.
Posted by Mike | August 25, 2012, 11:36 AM