
Project Euler & HackerRank Problem 17 Solution
Convert numbers to words
by {BetaProjects} | MAY 13, 2009 | Project Euler & HackerRankProject Euler Problem 17 Statement
Give a number, 0 ≤ N ≤ 1012, write out the equivalent value in English. This differs substantially from the original Project Euler problem by adapting it to the HackerRank requirements.
Solution
The intrinsic data
We create several lists to define all the English words that are required to spell any value less than one quintillion (1018). Lists ones and tens are permuted using the itertools.product function to generate the decades and compound numbers between 20 and 99. The words for the numbers 1 through 19 are then prepended to this list and stored in the units list. The intention was to have a one–to–one relationship with the index of the unit list and the corresponding number in written form.
You can extend the maximum value by simply adding other magnitudes to the thousands list.
The recursive function for hundreds
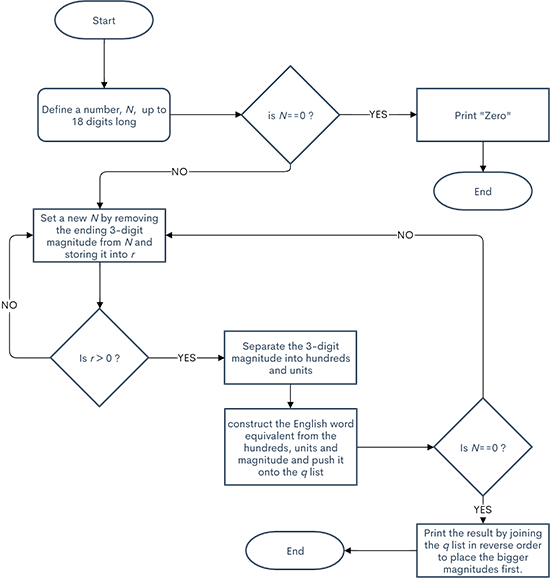
No matter how big the number is, it can be expressed by translating each 3–digit magnitude to a hundred designation (0–999) and then appending the appropriate magnitude (thousand’s) name to the end. For example, consider the number 194,382,426,112 expressed in English:
One Hundred Four Billion Three Hundred Eighty–Two Million Four Hundred Twenty–Six Thousand One Hundred Twelve
This pattern in large numbers allows us to create a recursive function (which could easily be replaced by a loop) to call upon itself until all the 3–digit magnitudes are processed. The q[] list will accumulate the word groups for each magnitude. Because we start with the lowest magnitude and work upwards, the list is joined in reverse order to place the larger magnitudes first.
Here is a flow chart to better explain the logic used to solve this problem:
HackerRank version
Python Source Code
Last Word
Other thousands groups: Quintillion 1018, Sextillion 1021, Septillion 1024, Octillion 1027, and even more here.