Project Euler Problem 6 Solution

Project Euler & HackerRank Problem 6 Solution

Sum square difference

by {BetaProjects} | MAY 17, 2009 | Project Euler & HackerRank

Project Euler Problem 6 Statement

The sum of the squares of the first ten natural numbers is 1² + 2² + … + 10² = 385.

The square of the sum of the first ten natural numbers is (1 + 2 + … + 10)² = 55² = 3025.

Hence the difference between the sum of the squares of the first ten natural numbers and the square of the sum is 3025 − 385 = 2640.

Find the difference between the sum of the squares of the first one hundred natural numbers and the square of the sum.

Solution

A simplified approach

print (sum(range(101))**2 − sum(i*i for i in range(101)))

Using loops to sum our objectives, and Python’s list comprehension structure, we can make a simple subtraction and print the difference. For the small upper bound of 100 it takes no time at all. But, this lacks the efficiency to solve the more demanding parameters of the HackerRank version. A better method will have to be discovered.

Calculating our objectives without looping

Solving this problem without using loops is achieved by implementing the following two established equations:
1. The sum of the first n natural numbers (called triangular numbers, used in Project Euler Problem 1):

\sum\limits_{i=1}^n i = \frac{n(n+1)}{2}

For a visual example of triangular numbers, imagine a set of bowling pins arranged in the traditional triangular pattern:

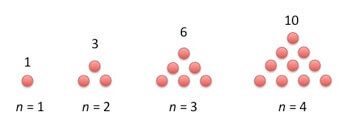
Triangular numbers

Let’s apply this equation to our example:
The square of the sum of the first ten natural numbers is 10(11)/2 = 55, and 552 = 3025 ✓.

2. The sum of the first n square numbers (square pyramidal numbers):

\sum\limits_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}

For a visual example of square pyramidal numbers, imagine a stack of marbles as shown below:

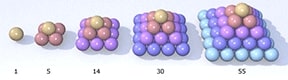
Square pyramidal numbers

Now, let’s apply this equation to our example:
The sum of the squares of the first 10 natural numbers is 10(11)(21)/6 = 385 ✓.

Finally, calculate the difference, 3025 – 385 = 2640 ✓. Knowing these equations is useful for solving other programming problems.

A compound formula

Now, I guess for the purists, one could perform the subtraction of these two summations and derive the following formula:

\frac{n(n-1)(n+1)(3n+2)}{12}

And giving it a try with our example: 10(9)(11)(32) / 12 = 2640 ✓.

HackerRank version

HackerRank logo

This program solves all test cases for Project Euler 6 on HackerRank

HackerRank requires you to solve up to 10,000 test cases with a higher limit of n ≤ 10,000. This is solved quickly by avoiding loops and using the closed–form calculations described above.

Python Source

  1. # -*- coding: utf-8 -*-
  2. n = int(input('first n natural numbers, n ='))
  3. print ("Difference: (Σn)² - Σn² =", n*(n-1)*(n+1)*(3*n+2)//12)
download Project Euler 6 Python source code Use this link to download the Project Euler Problem 6: Sum square difference.
run program on repl.it Run Project Euler Problem 6 using Python on repl.it

Last Word