
Project Euler 91: Right triangles with integer coordinates
Project Euler 91 Problem Description
Project Euler 91: The points P (x1, y1) and Q (x2, y2) are plotted at integer co-ordinates and are joined to the origin, O(0,0), to form ΔOPQ.
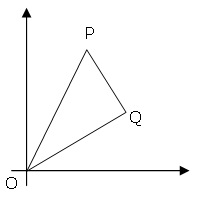
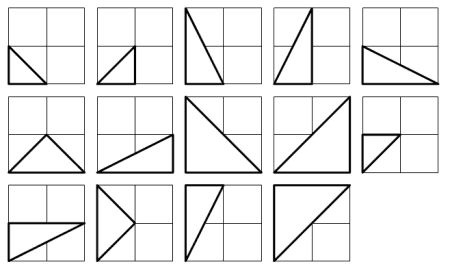
There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is,
0 ≤ x1, y1, x2, y2 ≤ 2.
Given that 0 ≤ x1, y1, x2, y2 ≤ 50, how many right triangles can be formed?
Analysis
There is a hyper series here…somewhere.
Data Table 1. Number of triangles from 0 ≤ x1, y1, x2, y2 ≤ {1..10}.
| N | # Triangles |
|---|---|
| 1 | 3 |
| 2 | 14 |
| 3 | 33 |
| 4 | 62 |
| 5 | 101 |
| 6 | 148 |
| 7 | 207 |
| 8 | 276 |
| 9 | 353 |
| 10 | 448 |
Now, we can remove 3n2 known triangles that have an edge on either axis.
Data Table 2. Number of triangles as above but with 3n2 contributing to sum
| N | 3N2 | From some other source | # Triangles |
|---|---|---|---|
| 1 | 3 | 0 | 3 |
| 2 | 12 | 2 | 14 |
| 3 | 27 | 6 | 33 |
| 4 | 48 | 14 | 62 |
| 5 | 75 | 26 | 101 |
| 6 | 108 | 40 | 148 |
| 7 | 147 | 60 | 207 |
| 8 | 192 | 84 | 276 |
| 9 | 243 | 110 | 353 |
| 10 | 300 | 148 | 448 |
Data Table 3. Number of triangles as above but with N2/2 contributing to sum
| N | 3N2 | N2/2 | From some other source | # Triangles |
|---|---|---|---|---|
| 1 | 3 | 0 | 0 | 3 |
| 2 | 12 | 2 | 0 | 14 |
| 3 | 27 | 4 | 2 | 33 |
| 4 | 48 | 8 | 6 | 62 |
| 5 | 75 | 12 | 14 | 101 |
| 6 | 108 | 18 | 22 | 148 |
| 7 | 147 | 24 | 36 | 207 |
| 8 | 192 | 32 | 52 | 276 |
| 9 | 243 | 40 | 70 | 353 |
| 10 | 300 | 50 | 98 | 448 |
Well, brute force until I figure out the series, which seems trivial but so far elusive. Still, good enough for even a more challenging problem set from HackerRank.
Project Euler 91 Solution
Runs < 0.001 seconds in Python 2.7. Use this link to get the Project Euler 91 Solution Python 2.7 source.
Use this link to get the Project Euler 91 Solution Python 2.7 source.
Afterthoughts
-
No afterthoughts yet.


Discussion
No comments yet.