Loading...
Project Euler 86: Exploring the shortest path from one corner of a cuboid to another
Problem Description
A spider, S, sits in one corner of a cuboid room, measuring 6 by 5 by 3, and a fly, F, sits in the opposite corner. By travelling on the surfaces of the room the shortest "straight line" distance from S to F is 10 and the path is shown on the diagram.
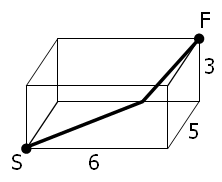
However, there are up to three “shortest” path candidates for any given cuboid and the shortest route is not always integer.
By considering all cuboid rooms with integer dimensions, up to a maximum size of M by M by M, there are exactly 2060 cuboids for which the shortest distance is integer when M=100, and this is the least value of M for which the number of solutions first exceeds two thousand; the number of solutions is 1975 when M=99.
Find the least value of M such that the number of solutions first exceeds one million.
Analysis
After discovering the sequence A143714 all that was required was to add the sequence until the sum exceeded the target, one million.
Project Euler 86 Solution
Runs < 0.800 seconds in Python 2.7.
Use this link to get the Project Euler 86 Solution Python 2.7 source.
Afterthoughts
- Reference: The On-Line Encyclopedia of Integer Sequences (OEIS) A143714: Number of pairs (a,b), 1 ≤ a ≤ b ≤ n, such that (a+b)^2+n^2 is a square.
Nice. I’m not sure I’m a fan of the “looking-up-the-sequence-school-of-problem-solving”. But, it’s sure effective.
Posted by jorge | November 23, 2013, 5:25 PMThere’s a mistake in your program.
The c += min(bc, a+1) – (bc+1)/2 should be c += min(bc, a+1) – int((bc+1)/2).
Posted by Spirit | May 3, 2011, 7:27 PMAll of the math in python is Integer unless specified explicitly. So, the int() function is not required in Python, but may be required for other languages.
I’ll change it as to remove any confusion. Thanks for the suggestion.
Posted by Mike | May 12, 2011, 12:17 PM