Project Euler 15: Find the number of routes from the top left corner to the bottom right corner in a rectangular grid.

Project Euler 15 Problem Description

Project Euler 15: Starting in the top left corner of a 2×2 grid, there are 6 routes (without backtracking) to the bottom right corner.

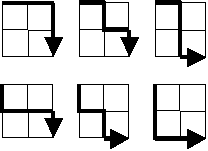
How many routes are there through a 20×20 grid?

Analysis

This question has been posed as: “Starting at the top left corner, how many ways through town are possible using only one-way streets and ending at the bottom right corner of a n x n grid?”

Another analogy might be: “Place a single rook on the top left corner of an empty chess board and count the number of tours to the bottom right corner moving only left and down.” This would assume an 8 × 8 grid.

This solution extends to solving n × m grids as well as the n × n grid by using a simple combination calculation. For example, the valid paths for a 2 × 2 grid shown in the example are the discreet (unique) permutations of {R, R, D, D}. We can list these as: {R, R, D, D}, {R, D, R, D}, {R, D, D, R}, {D, R, R, D}, {D, R, D, R}, and {D, D, R, R}. You must have n Rs (rights) and n Ds (downs) the order not being important and as long as you start from the top-left corner you will always end at the bottom-right corner.

For a 4 × 4 grid it would be the discreet permutations of {R, R, R, R, D, D, D, D} where any combination or 4 Rs and 4 Ds will always be a valid path. If the Rs are place randomly in 4 of the 8 slots first they can be considered independent and the Ds would be considered dependent because they have to be placed into the remaining open slots.

For example, placing the 4 Rs randomly in any of the available 8 slots as {R, _, R, R, _, R, _, _} will dictate where the Ds get placed as {R, D, R, R, D, R, D, D}. You end up with just ₈C₄ = 70 valid combinations.

Using the binomial coefficient

It could also be described as how many distinct ways can you shuffle the characters in the string “RRRRDDDD”.

Continuing our thinking from above we realize that determining the number of contiguous routes for a square grid (n × n) is the central binomial coefficient or the center number in the 2n^th row of Pascal's triangle. The rows start their numbering at 0.

The formula in general for any rectangular grid (n × m) using the notation for the binomial coefficient is:

The hackerRank Project Euler 15 version requires a thousand calculations for both rectangular and square grids up to 500 × 500 in less than a second.

This program and method
solves all test cases for
Project Euler 15 on HackerRank

Project Euler 15 Solution

Afterthoughts

• The Trinket math library’s factorial function doesn’t work, so we replaced it with a lambda function.
  
• Reference: The On-Line Encyclopedia of Integer Sequences (OEIS) A000984: Central binomial coefficients: C(2*n,n) = (2*n)!/(n!)^2.
  
• If we added the condition “contiguous paths which do not pass below the diagonal on an n x n grid” to our problem statement, we would use a Catalan number. It is calculated as: