
Project Euler 173: Using up to one million tiles find many different "hollow" square laminae can be formed.
Problem Description
We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry. For example, using exactly thirty-two square tiles we can form two different square laminae:
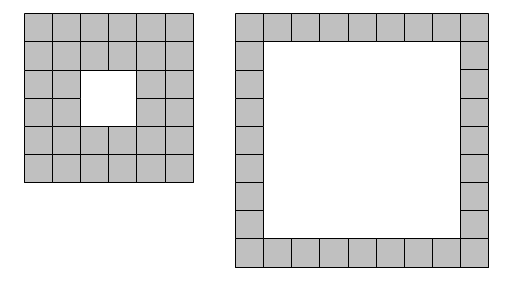
With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae.
Using up to one million tiles how many different square laminae can be formed?
Analysis
Ran a brute force for the first 10,000 tiles and found the series. So the next step is to form a generating function to calculate the answer, but, alas, this is unlikely to ever happen.
Project Euler 173 Solution
Runs < 0.001 seconds in Python 2.7. Use this link to get the Project Euler 173 Solution Python 2.7 source.
Use this link to get the Project Euler 173 Solution Python 2.7 source.
Afterthoughts
- See also, Project Euler 174 Solution:
Project Euler 173 Solution last updated


Discussion
No comments yet.